
Boj 8878, Hey, Better Bettor
이 문제를 해석해보자면
먼저, 나는 도박을 하는 중이고, 0$를 가지고 있다.
이때, 내가 도박에서 이기면 1$를 얻고, 지면 1$를 잃는다.
이길 확률은 p (0<=p<0.5)라고 한다.
근데, 이 도박장은 특이해서 잃은 금액의 x (0<=x<1)만큼을 환불해준다.
임의의 전략으로 도박을 진행할때, 어떻게 해야 기댓값이 가장 크겠는가?
(도박은 원할 때 그만둘 수 있다)
이 문제에서, 임의의 전략이 잘 와닿지 않는데, 전략이란, 일관된 선택, 즉 순서도 같은 것이다.
위 문제 상황에서 내가 선택할 수 있는건 그만두는 순간 말고는 없다.
즉, 임의의 전략이란, 게임을 그만두는 순간을 구체화한 것이다.
게임을 언젠가 그만둔다고 생각해보면, A$ 이상 잃었을 때 혹은 B$ 이상 얻었을 때 게임을 그만둔다고 생각해볼 수 있다.
그러면, 0$에서 시작하여 B$로 끝날 수도, -A$로 끝날 수도 있는 것이다.
B$로 끝날 확률을 P(0)라고 하자. 변수는 현재 가진 $이다.
P(x) = p * P(x+1) + (1-p) * P(x-1)이고,
일반항을 구해주면,
P(x) = (1-((1-p)/p)^(A+x)) / (1-((1-p)/p)^(A+B)) 가 된다.
이제, P(0)도 구했으니, 기댓값을 구할 수 있다.
P(0) 확률로 B$, 1-P(0) 확률로 A$이므로, 단순히 곱해주기만 하면 기댓값을 구할 수 있다.
Pred(A,B) = B*P(0) - A*(1-P(0))*(1-x)이 바로 기댓값에 대한 함수이다.
이제 이 문제는 Pred(A,B)를 최대화하는 0을 포함하는 자연수 A, B를 구하는 것이다.
A를 x축으로, B를 상수(슬라이드) 형태로 그래프를 그려보니까
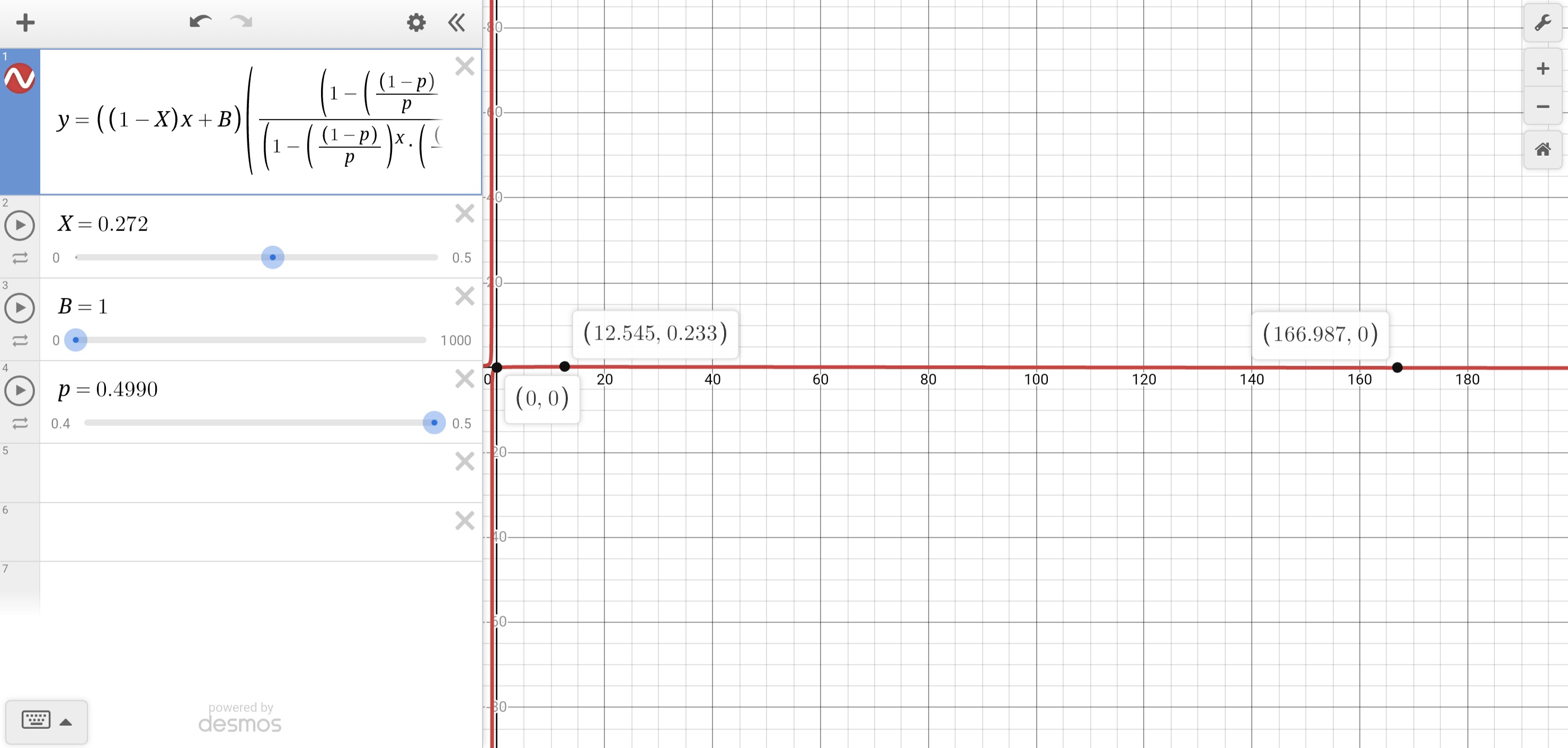




위의 그림을 보면, B가 증가함에 따라 최대점의 x좌표와 그때의 y값이 단조증가하다가
어느 순간 최대가 된 후, 다시 단조감소하는 것을 볼 수 있다.
계속 단조 감소 하면, 그 이후로는 (0,0) 이후로 x값이 증가하면서 y값은 계속 감소하는 단조감소 그래프가 된다.
이를 통해, B=0으로 초기화 한 상태에서, 최대점을 찾은 뒤로,
만약 B가 1 증가했을 때 최대점이 이전의 최대점보다 x좌표가 크다면
(==> 이전 최대점부터 탐색을 시작했을 때, 단조증가 함수여서 최대를 찍고 다시 단조감소 한다면)
최대점을 갱신해주고, 만약 최대점이 이전의 최대점보다 x좌표가 작다면
(==> 이전 최대점보다 y값도 감소했을 것임 ==> 이전 최대점이 이변수에 대한 진짜 최대점이 되는 것임)
그대로 탐색을 멈춘다.
그리고, 어떤 B에 대해 A에 대한 최대점을 찾을 때에도, 단조 증가 => 정지 => 단조 감소 그래프를 그리므로
Pred(A,B)에 비해 Pred(A+1,B)가 증가하면 계속 탐색, Pred(A+1,B)가 감소하면 탐색을 멈춘다.
이때, 엄청나게 정밀한 부동소수점 연산이 요구되기에 최대점 갱신은 그냥 기존의 부등식 연산을 사용하고,
단조 증가, 단조 감소 판별은 Epsilon을 정의하여 사용한다. ("최대점보다 Epsilon만큼 작으면 단조감소이다."와 같은 식으로 사용함)
이때, Epsilon은 크면 클수록 탐색을 더 진행한다는 뜻이 되므로
시간초과가 나게 하지 않으면서 최대한 크게 잡아준다. (나는 0.001로 사용했다.)
'C | C++ 알고리즘 & 자료구조' 카테고리의 다른 글
| Mertens Trick & Boj 17372, 16123 정리 공유 (0) | 2024.01.03 |
|---|---|
| boj 13728 행렬식과 GCD C++ 풀이 (1) | 2023.08.31 |
| boj 13308 주유소 C++ 풀이 (0) | 2023.01.30 |
| BOJ 2449 전구 풀이 (1) | 2023.01.29 |
| 가우스 소거법 with C++ (2) | 2023.01.29 |
